半導体のジャンクション温度(チャネル温度)を計算する場合、部品のデータシートに記載されている『熱抵抗』を用いますが、これが分かっているようでイマイチ分からない...。
という方も多いのではないでしょうか(自分もそうでした)。
『熱抵抗』といっても、部品のデータシートには、Rth(j-a)、Rth(j-c)、過渡熱抵抗、など...様々なパラメータが記載されています。
本記事は『熱抵抗』の考え方に重点をおいて構成し、分かりやすく解説していますので、一読いただければ、データシートがどのようなパラメータで表記してあっても正しくジャンクション温度を計算できるようになります。
✔️そもそも半導体のジャンクション温度とは?
✔️『熱抵抗』とは?
✔️『熱抵抗』を用いたジャンクション温度の計算方法
ジャンクション温度とは?
『熱抵抗』の話に入る前に、そもそも『ジャンクション温度』とはなにか、簡単に解説します。
半導体は、P型半導体とN型半導体によるpn接合で構成されます。
本記事で詳しく解説しませんが、半導体チップの整流作用(印加電圧に応じて電流を流したり止めたりするスイッチ作用)は、このpn接合によって成り立っています。
半導体に電流を流すと、pn接合の『接合部(ジャンクション)』が発熱します。
これを『ジャンクション温度』といいます。
半導体部品の温度定格はこの『ジャンクション温度(MOS FETの場合は『チャネル温度』)』で規定されます。
半導体部品を使用する際は、実使用条件(セットの負荷、環境)下で発生する『ジャンクション温度』が、データシートの定格を満足するか確認する必要があります。
ただ、当然のことながらチップの中にある微小なジャンクションの温度を熱電対などで直接測定することはできません。
ここで必要となるのが、『熱抵抗』という概念です。
熱抵抗の考え方
『熱抵抗』とは、熱の伝わりにくさを定量的に示す数値です。
考え方は電気抵抗(電流の流れにくさ)と同じで、値が大きいほど熱が伝わりにくくなります。
熱抵抗が分かれば、直接測定できないジャンクション温度を算出できます。
熱抵抗の概念
ある空間を熱が伝わった際の温度変化ΔTは、
ΔT = P x Rth で表すことができます。
ここで、Pは半導体の損失(によって発生する熱流)、Rthはその物体の熱抵抗です。
このΔTを求める式は、オームの法則で言うところの 電圧変化(降下)ΔV = I x R と同じ理屈です。
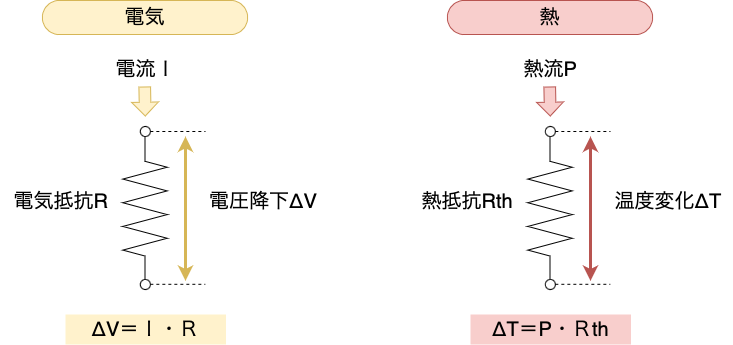
この式は、熱源の温度を直接測定できなくても、”測定可能な点”との間の熱抵抗が分かっていれば、熱源の温度を逆算できる、ということを意味します。
例えば下図において、測定点Aの温度をTa、熱源の温度をTbとすると、
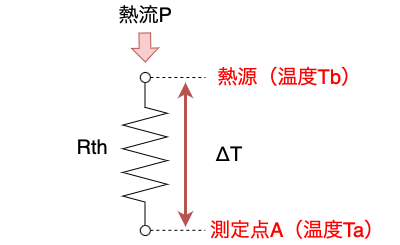
Tb=ΔT+Ta です。※Taは既知または、測定して得る。
ΔT=P・Rthなので、Tb=P・Rth+Ta となります。
この式が半導体のジャンクション温度を計算する上で基本となります。
熱抵抗の種類
半導体のデータシートには、大きく分けて下記のいずれか、または両方が記載されています。
Rth(j-c):ジャンクション-ケース間熱抵抗
半導体のジャンクションとケース(半導体パッケージの表面)間の熱抵抗です。
パッケージの形状に大きく依存します。
Rth(j-a):ジャンクション-大気(エア)間熱抵抗
半導体のジャンクションと大気間の熱抵抗です。
大気は、対象部品が置かれた空間の、十分に拡散された点を指します(部品が置かれた部屋の温度と思えば良いです)。
ジャンクション、ケース、大気および、それぞれの熱抵抗の関係を下図に示します。
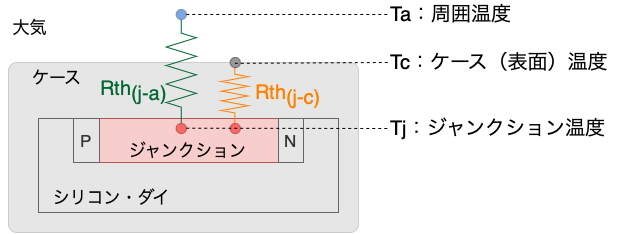
以下、これら熱抵抗を用いたジャンクション温度の計算方法を具体的に説明していきます。
ジャンクション温度の計算方法
上述した『ジャンクション-ケース間熱抵抗』、『ジャンクション-大気間熱抵抗』いずれかを用いて、ジャンクション温度を計算することができます。
どちらの熱抵抗を用いてもジャンクション温度の算出は可能ですが、それぞれ特徴がありますので、原理を分かった上で計算する必要があります。
ジャンクション-ケース間熱抵抗Rth(j-c)を用いた計算方法
ジャンクション温度は、ジャンクション-ケース間熱抵抗Rth(j-c)とケース温度Tcを用いて、下記のとおり計算できます。
Tj = P・Rth(j-c)+Tc

損失Pは部品種類によって求め方が異なりますが、例えばMOS FETであれば、
P = RON(オン抵抗)・ID(ドレイン電流)^2
などで求めます。
次に、実際にケース温度を測定してTcを得ます。
以上により、ジャンクション温度を算出できます。
ジャンクション-ケース間熱抵抗Rth(j-c)は、半導体部品のパッケージ内で放熱条件がほぼ完結するパラメータであるため、パッケージ外部の要因である『周囲の気流状態(気流が流れているか停滞しているか)』、『半田組成』、『パターンの形状および材料』、『基板の形状および材料』、等の影響を受けにくいです。
このため本測定方法は、後に解説するジャンクション-大気間熱抵抗を用いた計算方法と比較して、ケース温度の測定は面倒だが比較的正確なジャンクション温度を得られる、という特徴があります。
ジャンクション-大気間熱抵抗Rth(j-a)用いた計算方法
ジャンクション温度は、ジャンクション-大気間熱抵抗Rth(j-a)と、大気温度(周囲温度)Taを用いて、下記のとおり計算できます。
Tj = P・Rth(j-a)+Ta
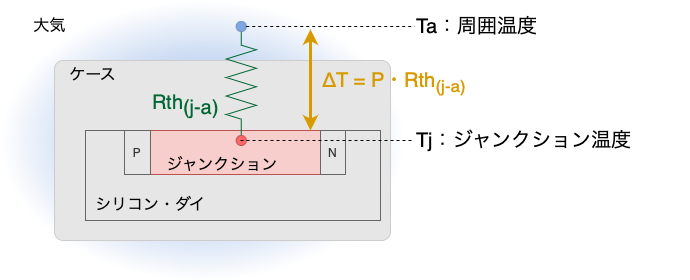
損失Pの求め方は前項ジャンクション-ケース間熱抵抗を用いた場合と同様です。
Taは「対象のデバイスが置かれた空間(自身の発熱の影響を受けない十分に広い空間)の温度(≒対象デバイスが置かれた部屋の室温)」です。
上述したケース温度は、デバイスに実使用条件と同等の負荷を与えた状態で温度上昇試験を実施して得る必要がありますが、Taはデバイスの温度上昇試験が不要(室温を測れば良いだけ)なので、容易に得ることができます。
つまり、本計算方法は想定した周囲温度条件におけるジャンクション温度を机上計算できる、と言えます。
ただし、ジャンクション-大気間は熱流経路がパッケージ外部の要因である『周囲の気流状態(気流が流れているか停滞しているか)』、『半田組成』、『パターンの形状および材料』、『基板の形状および材料』、等の影響を受けやすく、熱抵抗の値はこれら条件に大きく依存します。
(部品のデータシートに記載されているジャンクション-大気間熱抵抗の値は、メーカがある一定の条件で測定した結果であり、実際に使用したい条件での厳密な熱抵抗値を得ることは難しいです)
もう少し詳細を説明すると、下図のように、熱が伝搬する経路は複数あり、全体の熱抵抗は各経路の熱抵抗の合成になります(考え方は電気抵抗と同じ)。そして上述したとおり、各経路の熱抵抗(Rth(j-a)1〜3)はパッケージ外部の要因により変動します。

以上より、本算出手段は、計算結果の正確性に欠ける、といったデメリットもあります。
まとめ
半導体部品の熱抵抗には、『ジャンクション-ケース間熱抵抗:Rth(j-c)』と、『ジャンクション-大気間熱抵抗:Rth(j-a)』の両方あるいは、いずれかが記載されており、これらを使い分ける必要があります。
それぞれのメリット・デメリットを下表に示します。

部品を選定する際にざっくり使用可否を判断するためにはRth(j-a)を用いて簡易計算を、選定したデバイスを実際にセットに組み込んで評価する際にはRth(j-c)を用いて正確な計算を、といった具合に使い分けます。
データシートには、これらとは別に、過渡熱抵抗rthがありますが、こちらについては別の機会で解説します。



コメント